Concerning QM, GR and SR mathematics
When reading about spin, spacetime and particles and their antiparticles (inducing or needing negative time), for example, one can state that it all is about math. These entities or functions, and many more, are only “understood” or noticed in the QM, GR and SR formulas. Still, the math makes predictions; explains behavior, and so on in a very exact way. So, the math seems to be correct and confirmed in (almost?) all experiments and most observations made.
How come that these three physics fields at all need mathematics that almost no one can understand and relate to in our average “physical” world? Why is it so abstract, so difficult? One can give an example with the physics/ mathematical spacetime concept first proposed by the mathematician Hermann Minkowski in 1908. The leap from classical physics to “modern” early 20th century GR and SR physics has both revolutionized and made it more complex. Even if the complexity in physical math can be seen introduced with the four partial differential equations by the Scottish late 19th century physicist James Maxwell, with his equations about electromagnetism. Also the introduction of QM, quantum mechanics, at the early 20th century had this effect on the possibility to understand physics.
For example, the light cone model, used in the three physics fields, is drawn from the spacetime concept with a minor amount of dimensions than its theory says (three spatial dimensions and one time dimension). Instead it is visualized with two spatial (x, y, plane) and one time dimension. This is done because intellects better can picture it with only totally three dimensions. Even if you view the light cone in VR (virtual reality) it can only be schematically depicted with three dimensions.
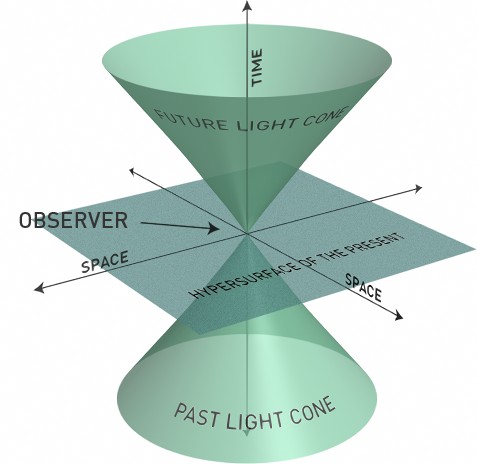
Illustration of a light cone (x, y, and time)
In math it’s rather easy for a trained mathematician to “work” with totally four dimensions (the true spacetime spatial constructed light cone). But in the real world almost no one, maybe even nobody, can understand the light cone in a true spatial sense. Hence it’s only possible to physically describe it with advanced math. And mathematics should always be a metaphor for true physics. Doesn’t this way of describing an event, E, and its causality using the light cone, only via math, turn on this order of first physics then math?
I cannot get rid of the suspicion that math (sometimes?) “lure” true physics into something it is not. Or more likely makes physics calculus a bit too complicated, than it has to be. Though most, maybe all, modern physics math is describing events in an excellent way and should be regarded as true physics. -This I am aware of.
However, I don’t believe Einstein himself truthfully understood the spacetime concept in GR or SR in a physical sense, merely in a metaphorically mathematical way. And that he often used metaphors in his reasoning is well known. He was though a schooled teacher and precise mathematician who normally worked with math as a tool for describing events and outcomes, for example. I mean that it’s easy to add time to the three spatial dimensions. To be at a place also incorporates the right time. And four dimensions are not that tough for an experienced mathematician. It’s only that reality is best visualized with 3 dimensions. The time adding component is not easy to view in a straight spatial manner. And this reflects in his GR and SR equations. The main formulas for linking the curvature of space to matter and energy establishing gravity are considered being very complex.
For example, the most famous formula taken from SR, the E=mc^2 uses speed ((m/s)^2) aka distance divided with time and indicates on his intricate way of involving space and time. In this Einstein is a genius. How he transformed mass, light, distance and time to this formula is even today a true physical enigma. However, the spacetime concept, among other central concepts, has without doubt made the need for high or extreme mathematics to be incorporated into physics. Maybe for better, maybe for worse. -Though we have be aware of that the concept of light cones was already present in the work of earlier physicists, such as Hermann Minkowski’s, introduction of spacetime as a unified four-dimensional framework combining space and time.
One, besides, has to be clear about that the space and time entities (meter & seconds) also are used separately in QM, GR and SR as they are normally understood. Still, how the combined entity, spacetime, in GR, for example, evokes/ holds spatial gravity is mysterious, even if the calculus always is precise.
Regards
/admin
